Vectors

Vectors are a fundamental mathematical concept which allow you to describe a direction and magnitude. In games and apps, vectors are often used to describe fundamental properties such as the position of a character, the speed something is moving, or the distance between two objects.

Vector arithmetic is fundamental to many aspects of computer programming such as graphics, physics, and animation, and it’s useful to understand it in depth to get the most out of Unity.

Vectors can be expressed in multiple dimensions, and Unity provides the Vector2, Vector3, and Vector4 classes for working with 2D, 3D, and 4D vectors. These three types of Vector classes all share many of the same functions, such as magnitude, so most of the information on this page applies to all three types of Vector unless otherwise specified.

This page provides an overview of the Vector classes and their common uses when scripting with them. For an exhaustive reference of every member of the vector classes, refer to the script reference pages for Vector2, Vector3 and Vector4.

Understanding vector arithmetic

Addition

When two vectors are added together, the result is equivalent to taking the original vectors as “steps”, one after the other. Note that the order of the two parameters doesn’t matter, since the result is the same either way.

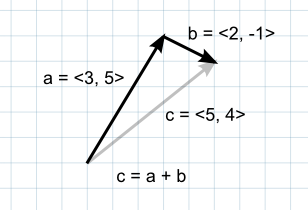
If the first vector is taken as a point in space then the second can be interpreted as an offset or “jump” from that position. For example, to find a point 5 units above a location on the ground, you could use the following calculation:

 var pointInAir = pointOnGround + new Vector2(0, 5);

If the vectors represent forces then it’s more intuitive to think of them in terms of their direction and magnitude (the magnitude indicates the size of the force). Adding two force vectors results in a new vector equivalent to the combination of the forces. This concept is often useful when applying forces with several separate components acting at once (for example, a rocket being propelled forward might also be affected by a crosswind).

The examples here use 2D vectors but the same concept applies to 3D and 4D vectors.

Subtraction

Vector subtraction is most often used to get the direction and distance from one object to another. Note that the order of the two parameters does matter with subtraction:

// The vector d has the same magnitude as c but points in the opposite direction.
var c = b - a;
var d = a - b;

As with numbers, adding the negative of a vector is the same as subtracting the positive.

// These both give the same result.
var c = a - b;
var c = a + -b;

The negative of a vector has the same magnitude as the original and points along the same line but in the exact opposite direction.

Direction and distance from one object to another

If one point in space is subtracted from another, then the result is a vector that “points” from one object to the other:

// Gets a vector that points from the player's position to the target's.
var heading = target.position - player.position;

As well as pointing in the direction of the target object, this vector’s magnitude is equal to the distance between the two positions. You may need a “normalized” vector giving the direction to the target, but with a fixed distance (say for directing a projectile). You can normalize a vector by dividing it by its own magnitude:

var distance = heading.magnitude;
var direction = heading / distance; // This is now the normalized direction.

This approach is preferable to using both the magnitude and normalized properties separately, since they are both quite CPU-hungry (they both involve calculating a square root).

If you only need to use the distance for comparison (for a proximity check, say) then you can avoid the magnitude calculation altogether. The sqrMagnitude property gives the square of the magnitude value, and is calculated like the magnitude but without the time-consuming square root operation. Rather than compare the magnitude against a known distance, you can compare the squared magnitude against the squared distance:

if (heading.sqrMagnitude < maxRange * maxRange) {
    // Target is within range.
}

This is much more efficient than using the true magnitude in the comparison.

Sometimes, when working in 3D, you might need an “overground heading” to a target. For example, imagine a player standing on the ground who needs to approach a target floating in the air. If you subtract the player’s position from the target’s then the resulting vector will point upwards towards the target. This is not suitable for orienting the player’s transform since they will also point upwards; what is really needed is a vector from the player’s position to the position on the ground directly below the target. You can get this by taking the result of the subtraction and setting the Y coordinate to zero:

var heading = target.position - player.position;
heading.y = 0;  // This is the overground heading.

Scalar multiplication and division

When discussing vectors, it is common to refer to an ordinary number (for example, a float value) as a scalar. The meaning of this is that a scalar only has “scale” or magnitude whereas a vector has both magnitude and direction.

Multiplying a vector by a scalar results in a vector that points in the same direction as the original. However, the new vector’s magnitude is equal to the original magnitude multiplied by the scalar value.

Likewise, scalar division divides the original vector’s magnitude by the scalar.

These operations are useful when the vector represents a movement offset or a force. They allow you to change the magnitude of the vector without affecting its direction.

When any vector is divided by its own magnitude, the result is a vector with a magnitude of 1, which is known as a normalized vector. If a normalized vector is multiplied by a scalar then the magnitude of the result will be equal to that scalar value. This is useful when the direction of a force is constant but the strength is controllable (for example, the force from a car’s wheel always pushes forwards but the power is controlled by the driver).

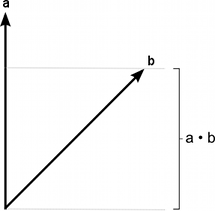
Dot product

The dot product takes two vectors and returns a scalar. This scalar is equal to the magnitudes of the two vectors multiplied together and the result multiplied by the cosine of the angle between the vectors. When both vectors are normalized, the cosine essentially states how far the first vector extends in the second’s direction (or vice-versa - the order of the parameters doesn’t matter).

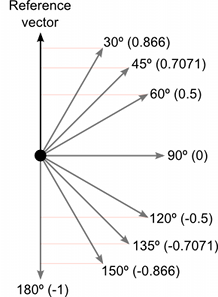
Below you can see a comparison of how vectors of varying angles compared with a reference vector return a dot product value between 1 and –1 :

The dot product is a mathematically simpler operation than calculating the cosine, so it can be used in place of the Mathf.Cos function or the vector magnitude operation in some circumstances (it doesn’t do exactly the same thing but sometimes the effect is equivalent). However, calculating the dot product function takes much less CPU time and so it can be a valuable optimization.

The dot product is useful if you want to calculate the amount of one vector’s magnitude that lies in the direction of another vector.

For example, a car’s speedometer typically works by measuring the rotational speed of the wheels. The car may not be moving directly forward (it may be skidding sideways, for example) in which case part of the motion will not be in the direction the car is facing - and so won’t be measured by the speedometer. The magnitude of an object’s rigidbody.velocity vector will give the speed in its direction of overall motion but to isolate the speed in the forward direction, you should use the dot product:

var fwdSpeed = Vector3.Dot(rigidbody.velocity, transform.forward);

The direction can be anything you like but the direction vector must always be normalized for this calculation. Not only is the result more accurate than the magnitude of the velocity, it also avoids the slow square root operation involved in finding the magnitude.

Cross product

The cross product is only meaningful for 3D vectors. It takes two 3D vectors as input and returns another 3D vector as its result.

The result vector is perpendicular to the two input vectors. You can use the “right hand screw rule” to remember the direction of the output vector from the ordering of the input vectors. If you can curl your fingers in the order of the input vectors, your thumb points in the direction of the output vector. If the order of the parameters is reversed then the resulting vector will point in the exact opposite direction but will have the same magnitude.

The magnitude of the result is equal to the magnitudes of the input vectors multiplied together and then that value multiplied by the sine of the angle between them. Some useful values of the sine function are shown below:-

The cross product can seem complicated since it combines several useful pieces of information in its return value. However, like the dot product, it is very efficient mathematically and can be used to optimize code that would otherwise depend on slower transcendental functions such as sine and cosine.

Computing a normal/perpendicular vector

A “normal” vector (ie. a vector perpendicular to a plane) is required frequently during meshThe main graphics primitive of Unity. Meshes make up a large part of your 3D worlds. Unity supports triangulated or Quadrangulated polygon meshes. Nurbs, Nurms, Subdiv surfaces must be converted to polygons. More info
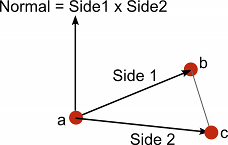
See in Glossary generation and is also useful in path following and other situations. Given three points in the plane, say the corner points of a mesh triangle, you can find the normal as follows: - Pick one of the three points - Subtract it from each of the two other points separately (resulting in two new vectors, “Side 1” and “Side 2”) - Calculate the cross product of the vectors “Side 1” and “Side 2” - The result of the cross product is a new vector that is perpendicular to the plane the three original points lie on - the “normal”.

Vector3 a;
Vector3 b;
Vector3 c;

Vector3 side1 = b - a;
Vector3 side2 = c - a;

Vector3 normal = Vector3.Cross(side1, side2);

The “left hand rule” can be used to decide the order in which the two vectors should be passed to the cross product function. As you look down at the top side of the surface (from which the normal will point outwards) the first vector should sweep around clockwise to the second:

The result will point in exactly the opposite direction if the order of the input vectors is reversed.

For meshes, the normal vector must also be normalized. This can be done with the normalized property, but there is another trick which is occasionally useful. You can also normalize the perpendicular vector by dividing it by its magnitude:-

float perpLength = perp.magnitude;
perp /= perpLength;

Another useful note is that the area of the triangle is equal to perpLength / 2. This is useful if you need to find the surface area of the whole mesh or want to choose triangles randomly with probability based on their relative areas.