- Unity User Manual 2020.2
- Física
- 3D Physics for object-oriented projects
- Continuous collision detection (CCD)
Continuous collision detection (CCD)
CCD ensures that fast-moving bodies collide with objects instead of passing, or tunnelling, through those objects. Unity provides the following CCD methods:
To use sweep-based CCD, select a RigidBody in the Inspector window and set Collision Detection to Continuous or Continuous Dynamic. For speculative CCD, set Collision Detection to Continuous Speculative.
Sweep-based CCD
Sweep-based CCD uses a Time Of Impact (TOI) algorithm to compute potential collisions for an object by sweeping its forward trajectory using its current velocity. If there are contacts along the object’s moving direction, the algorithm computes the time of impact and moves the object until that time. The algorithm can perform sub steps from that time onwards, computing the velocity after TOI then re-sweep, at the expense of more CPU cycles.
However, because this method relies on linear sweep, it ignores the body’s angular motion, which can cause tunnelling effects when objects are rotating at speed. For example, the flipper in a pinball machine is fixed at one end and rotates around a fixed point. The flipper only has angular motion and no linear motion. Therefore, it can easily miss the collision with the pinball:

Another issue with this method is performance. If you have a large number of high-speed objects with CCD in close proximity, the CCD overhead increases quickly because of the extra sweeping, and the physics engine has to perform more CCD sub-steps.
Speculative CCD
Speculative CCD works by increasing an object’s broad-phase axis-aligned minimum bounding box (AABB), based on the object’s linear and angular motion. The algorithm is speculative because it picks all potential contacts during the next physics step. All contacts are then fed into the solver, which makes sure that all contact constraints are satisfied so that an object does not tunnel through any collision.
The following diagram shows how a sphere moving from t0 could have an expected position at t1 if there were no walls in its path. By inflating the AABB with its target pose, the speculative algorithm picks up two contacts with the n1 and n2 normals. The algorithm then tells the solver to respect those contacts so that the sphere doesn’t tunnel through the walls.
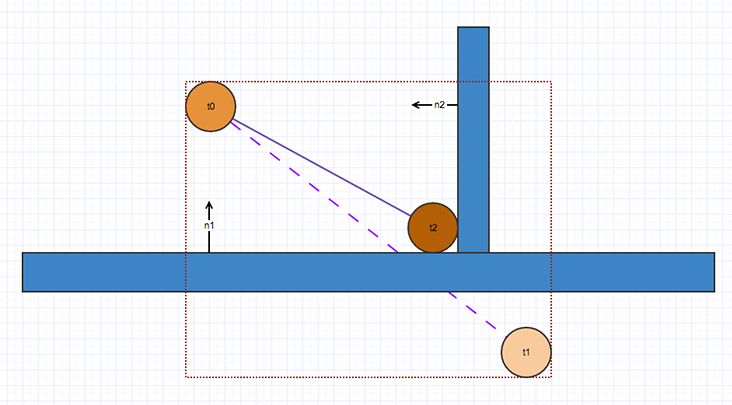
Inflated AABB based on current velocity helps detect all potential contacts along the moving trajectory, which enables the solver to prevent tunnelling.
Speculative CCD is generally cheaper than the sweep-based method because contacts are only computed during the collision detection phase, not during the solving and integrating phase. Also, because Speculative CCD expands the broad-phase AABB based on the object’s linear and angular motion, it finds the contacts that sweep-based CCD can miss.

However, speculative CCD can cause a ghost collision, where an object’s motion is affected by a speculative contact point when it shouldn’t be. This is because speculative CCD collects all potential contacts based on the closest point algorithm, so the contact normal is less accurate. This can often make high speed objects slide along tessellated collision features and jump up, even though they shouldn’t. For example, in the following diagram, a sphere starts at t0 and moves horizontally towards the right, with a predicted position at t1 after integration. An inflated AABB overlaps the boxes b0 and b1, and the CCD yields two speculative contacts at c0 and c1. Because speculative CCD generates contacts using the closest point algorithm, c0 has a very inclined normal, which appears to be a ramp to the solver.
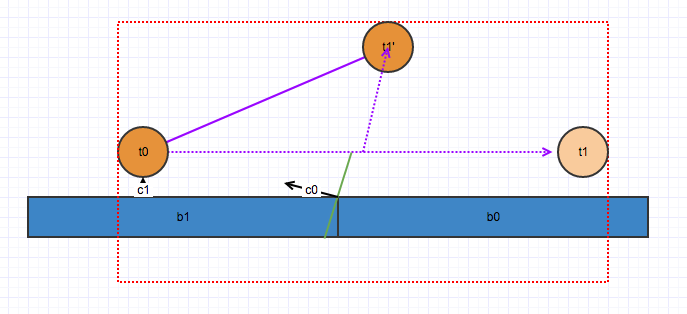
Such a very inclined normal causes t1 to jump upward after integration, rather than moving straight forward:
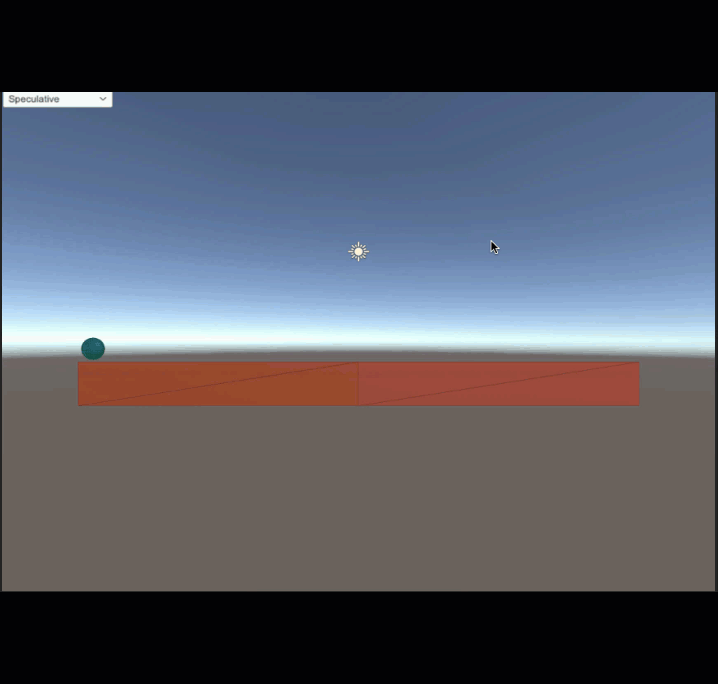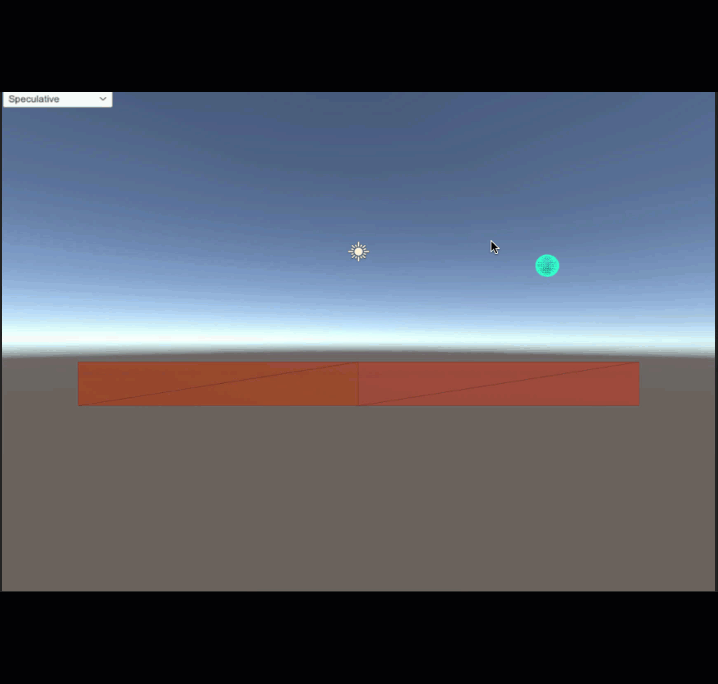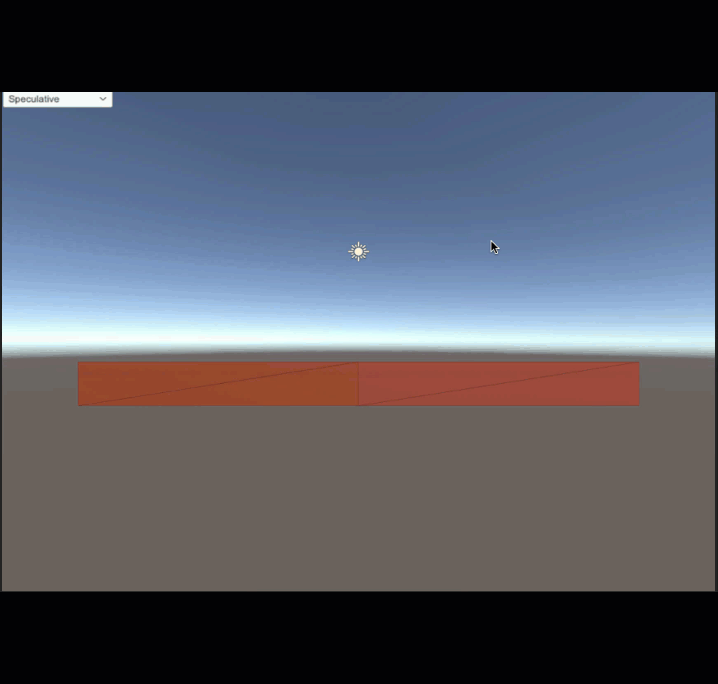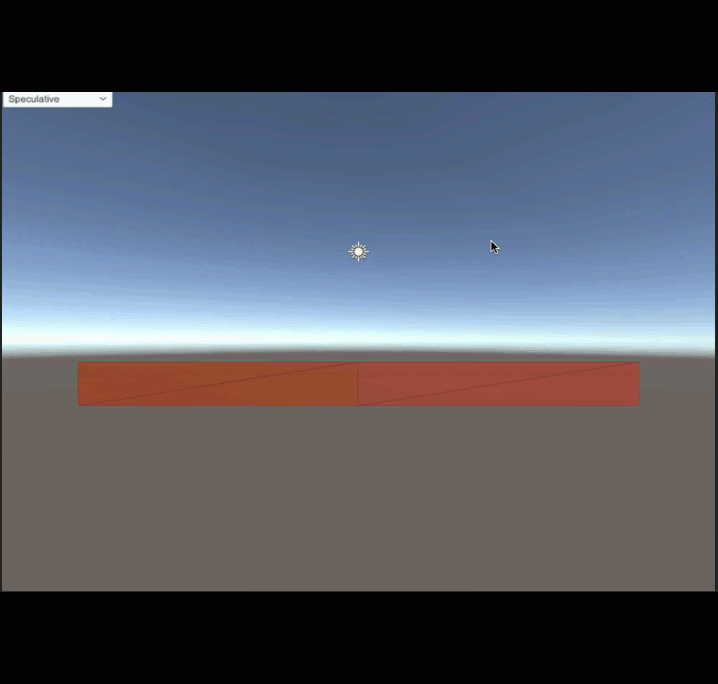
Speculative CCD can also cause tunneling because speculative contacts are only computed during the collision detection phase. During contact solving, if an object gains too much energy from the solver, it may end up outside the initial inflated AABB after integration. If there are collisions just outside the AABB, the object will tunnel right though.
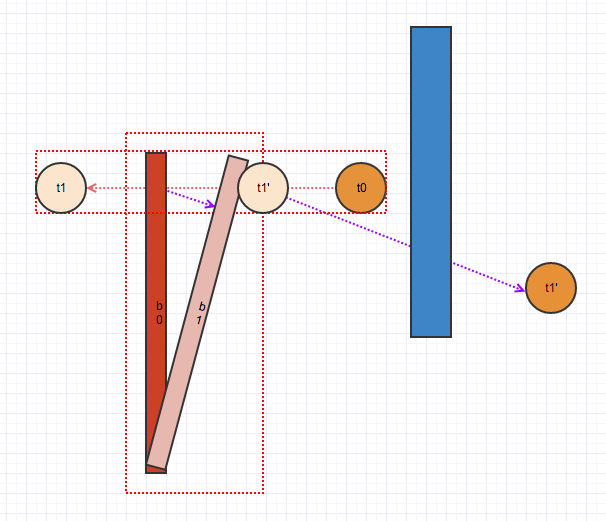
For example, the following diagram shows a sphere is moving left from t0 while a stick is rotating clockwise. If the sphere gains too much energy from the impact, it may end up exiting the inflated AABB (red dotted rectangle) at t1. If there are collisions just outside the AABB, as shown by the blue box below, the sphere may end up tunneling right through it. This is because the solver only computes contacts inside the inflated AABB, and collision detection isn’t performed during the solving and integrating phase.
2018–10–12 Page published
Speculative collision detection added in 2018.3 NewIn20183